Curious about Classical Mechanics? Check out these mind-boggling problems with step-by-step solutions!

Classical mechanics, also known as Newtonian mechanics, is a fundamental branch of physics that deals with the motion of objects, understanding forces acting on them, and predicting their future positions. It is an integral part of physics education and forms the foundation for more advanced topics such as quantum mechanics and general relativity.

Are you a physics enthusiast or a student struggling to wrap your head around classical mechanics concepts? Look no further! In this article, we have compiled a series of classical mechanics problems along with their detailed solutions to help you gain a deep understanding of this fascinating subject.

1. Problem: Projectile Motion

A cannon on a hill fires a projectile at an angle of 35 degrees with the horizontal. If the initial velocity of the projectile is 100 m/s, what is the maximum height reached by the projectile and the total time of flight? Provide a step-by-step solution to explain your answer.

Classical Mechanics: Problems with solutions (IOP Expanding Physics Book 2)

by John M. Howie(Kindle Edition)

4.4 out of 5

Language	:	English
File size	:	13110 KB
Text-to-Speech	:	Enabled
Enhanced typesetting	:	Enabled
Print length	:	485 pages
Screen Reader	:	Supported

FREE

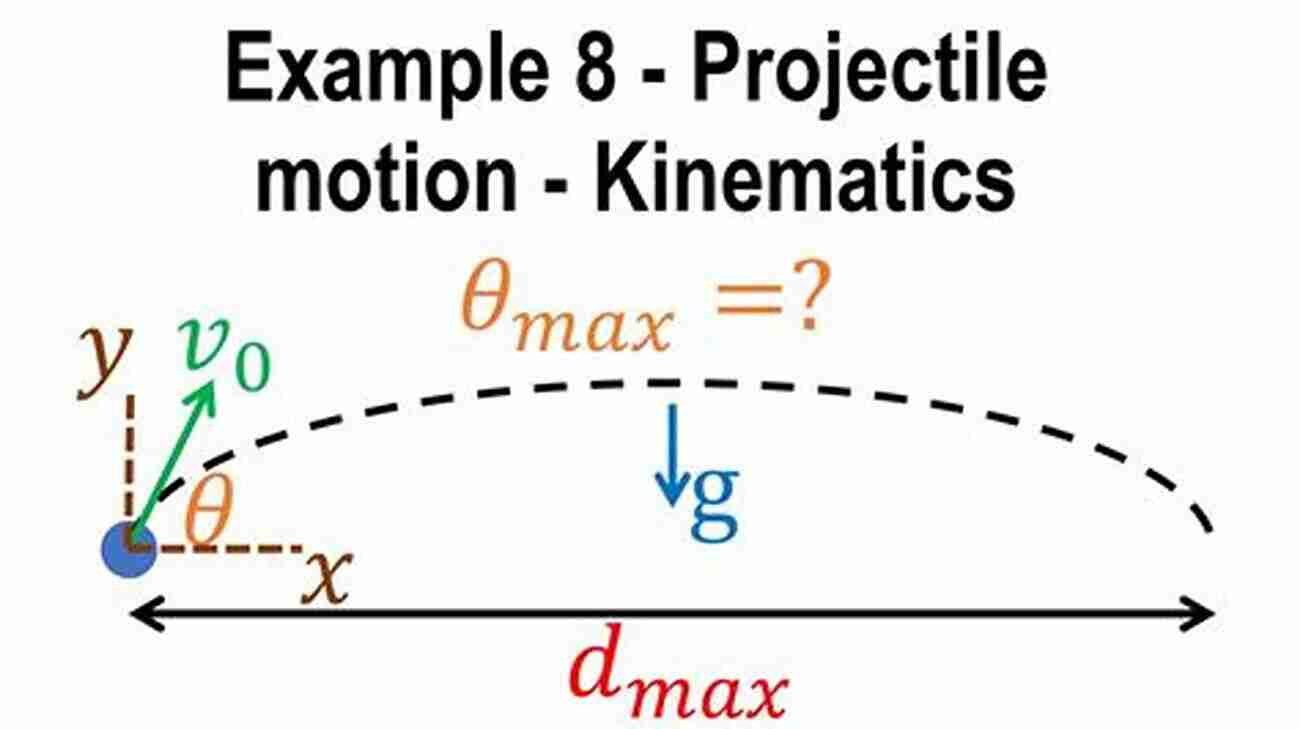
Solution: To solve this problem, we need to break the initial velocity into its horizontal and vertical components. The horizontal component remains constant, while the vertical component changes due to gravity. By using kinematic equations and applying the laws of motion, we can find the maximum height reached and the time of flight.

Step 1: Determine the vertical component of the initial velocity using sine of the angle of projection:

Vertical component = Initial velocity * sin(angle)

Vertical component = 100 m/s * sin(35 degrees)

Step 2: Calculate the time taken to reach maximum height using the equation:

Time of flight = (2 * Vertical component) / gravitational acceleration

Step 3: Use the known values to calculate the maximum height:

Maximum height = (Vertical component * time of flight) - (0.5 * gravitational acceleration * (time of flight)^2)

By substituting the values and solving these equations, we find that the maximum height reached by the projectile is approximately 520 meters, and the total time of flight is around 10 seconds.

2. Problem: Newton's Laws

A car of mass 1500 kg is initially at rest. A constant force of 2000 N is applied to it for a duration of 10 seconds. What is the final velocity of the car and the distance covered during this time? Justify your answer using Newton's laws of motion.

Solution: Newton's second law states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. By applying this law and using kinematic equations, we can determine the final velocity and the distance covered by the car.

Step 1: Calculate the acceleration of the car:

Acceleration = Net force / Mass

Acceleration = 2000 N / 1500 kg

Step 2: Use the equation of motion to find the final velocity:

Final velocity = Initial velocity + (Acceleration * Time)

Since the car is initially at rest, the initial velocity is 0 m/s.

Final velocity = 0 m/s + (Acceleration * 10 seconds)

Step 3: Determine the distance covered by the car:

Distance = (Initial velocity * Time) + (0.5 * Acceleration * (Time^2))

Since the car is initially at rest, the initial distance is 0 meters.

Distance = 0 m + (0.5 * Acceleration * (Time^2))

After calculating these equations, we find that the final velocity of the car is 13.33 m/s, and the distance covered during this time is approximately 666.67 meters.

3. Problem: Conservation of Energy

A 2 kg block is initially at rest on a frictionless inclined plane. The angle of inclination is 30 degrees. What is the speed of the block when it reaches the bottom of the incline? Consider the conservation of energy principle to justify your answer.

Solution: According to the conservation of energy principle, the sum of potential energy and kinetic energy remains constant in a closed system. By applying this principle and understanding the relationship between potential and kinetic energy, we can determine the final speed of the block.

Step 1: Calculate the potential energy at the initial position using the equation:

Potential energy = Mass * Gravity * Height

Potential energy = 2 kg * 9.8 m/s^2 * (Height * sin(angle))

Step 2: Determine the kinetic energy at the bottom of the incline:

Since there is no loss of energy due to friction or other factors, the initial potential energy is converted entirely into kinetic energy at the bottom.

Kinetic energy = Potential energy at the initial position

1/2 * Mass * (Speed^2) = Potential energy at the initial position

Step 3: Solve the equation to find the final speed of the block:

Speed = sqrt((2 * Potential energy) / Mass)

After performing the calculations, we find that the speed of the block when it reaches the bottom of the incline is approximately 6.26 m/s.

By tackling these classical mechanics problems, you can develop a strong foundation in this field. Practicing such problems will enhance your analytical skills, critical thinking abilities, and problem-solving techniques.

If you have a passion for physics and want to explore more classical mechanics problems, IOP Expanding Physics is an excellent resource to expand your knowledge. They offer a wide range of physics-related materials, including textbooks, research papers, and educational resources to help you excel in your studies.

So, what are you waiting for? Dive into the world of classical mechanics and conquer its challenges one problem at a time!

Classical Mechanics: Problems with solutions (IOP Expanding Physics Book 2)

by John M. Howie(Kindle Edition)

4.4 out of 5

Language	:	English
File size	:	13110 KB
Text-to-Speech	:	Enabled
Enhanced typesetting	:	Enabled
Print length	:	485 pages
Screen Reader	:	Supported

FREE

Essential Advanced Physics is a series comprising four
parts: Classical Mechanics, Classical Electrodynamics, Quantum Mechanics and
Statistical Mechanics. Each part consists of two volumes, Lecture notes and Problems
with solutions, further supplemented by an additional collection of test
problems and solutions available to qualifying university instructors. This volume, Classical
Mechanics: Problems with solutions contains detailed model
solutions to the exercise problems formulated in the companion Lecture notes
volume. In many cases, the solutions include
result discussions that enhance the lecture material. For the reader’s
convenience, the problem assignments are reproduced in this volume.